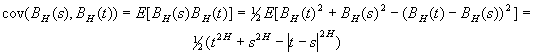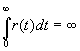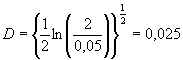Анализ свойства самоподобия трафика
веб-ресурса http://www.kp.karelia.ru
Оглавление
ВВЕДЕНИЕ
1 Самоподобные
процессы
1.1 Автокорреляционная функция
1.2 Самоподобный процесс
1.3 Долговременная зависимость
1.4 Распределения с тяжелыми хвостами
1.5 Методы оценки тяжести хвоста
1.6 Критерий согласия Колмогорова-Смирнова
2 Исследование
сетевого трафика на примере веб-сервера
2.1 Обзор существующих работ
2.2 Характеристики объекта изучения
2.3 Предпосылки
2.4 Распределение с тяжелым хвостом
2.5 Проверка гипотезы о виде функции
распределения
2.6 Проверка структуры на самоподобие
2.7 Долговременная зависимость
Заключение
Список
литературы
Приложение
1 динамика запросов
Приложение 2 Автокорреляционная функция
Долгое время считалось, что природа сетевого трафика соответствует
Пуассоновскому процессу. Со временем количество исследований и измерений
характеристик сетевого потока возрастало. В результате было замечено, что не
всегда поток пакетов в локальной или глобальной сети можно моделировать с
использованием Пуассоновского процесса. Таким образом, множество задач,
возникающих при исследовании трафика сети, пополнилось вопросом о характере
процесса движения пакетов по сети. Эта задача успешно рассматривается многими
учеными ведущих Университетов и Исследовательских центров мира [7], [9]. Первым и важным этапом этой работы стало
создание модели, характеризующей поведение сетевого трафика. На сегодняшний
день, существует вывод о том, что поведение сетевого трафика успешно
моделируется при помощи так называемого самоподобного процесса. Свойство
самоподобия ассоциируется с одним из типов фрактала, то есть, при изменении
шкалы корреляционная структура самоподобного процесса остается неизменной.
Теория самоподобных стохастических процессов не так хорошо развита, как
теория Пуассоновских процессов. Но, учитывая то, что самоподобные модели более
точно характеризуют поведение сетевого потока, чем пуассоновские модели, важной
задачей стала разработка инструментальных средств для понимания самоподобных
процессов, и для синтеза искусственного сетевого трафика, который отражает
основные характеристики этих процессов. Сегодня существует ряд таких алгоритмов
[8].
Далее, построенная самоподобная модель процесса движения пакетов в сети
требует неоднократной проверки с использованием реальных данных, измеренных для
различных сетей. Исследованию должны быть подвергнуты как локальные, так и
глобальные сети. Более того, возникает очень интересный вопрос об объяснении
возникновения именно свойства самоподобия трафика. Очень интересная работа была
проведена Университетом Бостона, а именно Марком Кровелла и Айзером Беставросом,
где показывается, что самоподобие в веб-трафике может быть объяснено
распределением размеров переданного документа, эффектом кэширования и
настройках пользователя по передаче файла, человеческим фактором, а также
суперпозицией множества таких передач в локальной сети [4].
В
представленной работе основной задачей является подтверждение самоподобия
веб-трафика, основанное на измерениях характеристик реального сетевого ресурса.
В качестве объекта исследования выбран процесс посещения веб-ресурса глобальной
сети. Рассматривается период существования ресурса длиной четыре месяца с 1
февраля 2001 года по 30 мая 2001 года. Фиксируемые характеристики – это
количество посетителей в течение часа. Таким образом, рассматриваемый временной
ряд содержит порядка 3 000 событий.
Структура
данной работы содержит две основные части. Первые две главы являются
необходимой теоретической основой для изучения самоподобных процессов. Здесь описаны определения и
свойства таких важных понятий, как временной ряд, автокорреляционная функция,
самоподобие, долговременная зависимость, распределение с тяжелым хвостом,
методы оценки тяжести хвоста, а так же небольшой обзор уже существующих
разработок в области исследования поведения сетевого трафика. Следующая глава содержит, описание характеристик
объекта исследования, а так же подробный ход проведения анализа трафика сети и
является второй основной частью представленной работы.
Подобный
анализ может быть так же проведен для других характеристик трафика, например
размеров передаваемых файлов, времени подачи запроса и времени выполнения.
1.1
Автокорреляционная функция
Периодическая зависимость представляет собой общий тип
компонент временного ряда. Можно легко видеть, что каждое наблюдение очень
похоже на соседнее; дополнительно, имеется повторяющаяся периодическая
составляющая, это означает, что каждое наблюдение также похоже на наблюдение,
имевшееся в том же самое время период назад. В общем, периодическая зависимость
может быть формально определена как корреляционная зависимость порядка k между
каждым i-м элементом ряда и (i-k)-м элементом. Ее можно измерить с помощью
автокорреляции (т.е. корреляции между самими членами ряда); k обычно называют
лагом (иногда используют эквивалентные термины: сдвиг, запаздывание). Если
ошибка измерения не слишком большая, то периодичность можно определить
визуально, рассматривая поведение членов ряда через каждые k временных единиц.
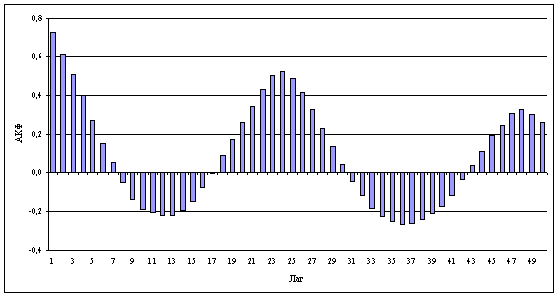
Рисунок 1.1 Автокоррелограмма
Периодические составляющие временного ряда могут быть найдены с
помощью коррелограммы. Коррелограмма (автокоррелограмма) показывает численно и
графически автокорреляционную функцию (AКФ), иными словами коэффициенты
автокорреляции для последовательности лагов из определенного диапазона (Рис.
1.1). На коррелограмме обычно отмечается диапазон в размере двух стандартных
ошибок на каждом лаге, однако обычно величина автокорреляции более интересна,
чем ее надежность, потому что интерес в основном представляют очень сильные (а,
следовательно, высоко значимые) автокорреляции.
При изучении коррелограмм следует помнить, что
автокорреляции последовательных лагов формально зависимы между собой.
Рассмотрим следующий пример. Если первый член ряда тесно связан со вторым, а
второй с третьим, то первый элемент должен также каким-то образом зависеть от
третьего и т.д. Это приводит к тому, что периодическая зависимость может
существенно измениться после удаления автокорреляций первого порядка, (т.е.
после взятия разности с лагом 1).
Другой полезный метод исследования периодичности состоит в
исследовании частной автокорреляционной функции (ЧАКФ), представляющей собой
углубление понятия обычной автокорреляционной функции. В ЧАКФ устраняется
зависимость между промежуточными наблюдениями (наблюдениями внутри лага).
Другими словами, частная автокорреляция на данном лаге аналогична обычной
автокорреляции, за исключением того, что при вычислении из нее удаляется
влияние автокорреляций с меньшими лагами. На лаге 1 (когда нет промежуточных
элементов внутри лага), частная автокорреляция равна, очевидно, обычной
автокорреляции. На самом деле, частная автокорреляция дает более
"чистую" картину периодических зависимостей.
Как отмечалось выше, периодическая составляющая для данного
лага k может быть удалена взятием разности соответствующего порядка. Это
означает, что из каждого i-го элемента ряда вычитается (i-k)-й элемент. Имеются
два довода в пользу таких преобразований.
Во-первых, таким образом можно определить скрытые
периодические составляющие ряда. Напомним, что автокорреляции на
последовательных лагах зависимы. Поэтому удаление некоторых автокорреляций
изменит другие автокорреляции, которые, возможно, подавляли их, и сделает
некоторые другие сезонные составляющие более заметными. Во-вторых, удаление
периодических составляющих делает ряд стационарным , что необходимо
для применения некоторых методов анализа.
Процесс
передачи данных в сети часто рассматривается в соответствии с Пуассоновским
процессом. Но совершенствуемые средства исследования локальной и глобальной
сети (LAN и
WAN)
делают возможным наблюдения за большими объемами данных. Анализ этих данных
показывает, что классическая теория очередей предполагает легкие хвосты и
независимость в применении к ним. Огромные потоки данных LAN трафика позволяют
проследить долговременную зависимость, то есть процесс самоподобия. Сейчас
можно утверждать, что самоподобие является существенным фактором сетевого
моделирования.
Рассмотрим
основные определения, необходимые для понимания явления самоподобия[4].
Процесс
в дискретном времени 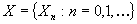 - стационарный
второго порядка, если выполняются условия:
- стационарный
второго порядка, если выполняются условия:
(1) постоянное
среднее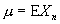 ,
, 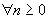
(2) конечная
дисперсия 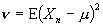 ,
, 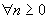
Более
того, 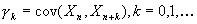 - автоковариационная
функция процесса зависит только от k и не зависит от n. Обозначим
- автоковариационная
функция процесса зависит только от k и не зависит от n. Обозначим 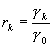 - автокорреляционная
функция.
- автокорреляционная
функция.
Построим
новый стационарный процесс второго порядка 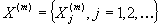 , получаемый разделением последовательности значений
данного процесса X
на блоки размера m.
То есть построим так называемый агрегированный процесс.
, получаемый разделением последовательности значений
данного процесса X
на блоки размера m.
То есть построим так называемый агрегированный процесс.
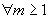
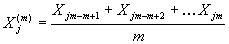 ,
, 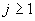 .
.
Рассмотрим понятие самоподобного процесса для
непрерывного и дискретного случаев.
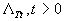 – самоподобный
процесс с параметром H, если
распределения
– самоподобный
процесс с параметром H, если
распределения 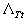 и
и 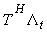 эквивалентны для
любого Т>0.
эквивалентны для
любого Т>0.
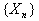 последовательность
случайных величин с конечным математическим ожиданием
последовательность
случайных величин с конечным математическим ожиданием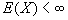 и дисперсией
и дисперсией 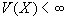 называется самоподобной
с параметром Н, если для каждого m=1,2,... последовательности
называется самоподобной
с параметром Н, если для каждого m=1,2,... последовательности
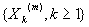 и
и 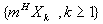
имеют одинаковые конечномерные распределения.
Процесс
будет асимптотически самоподобным, если ковариационная функция
приближается функцией следующего вида:
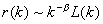 ,
,
где
параметр 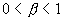 , L(k) – мало меняющаяся
функция.
, L(k) – мало меняющаяся
функция.
Для
процесса с долговременной зависимостью условие 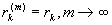 означает, что
для больших m,
означает, что
для больших m,
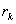 не зависит от
m. В этом случае,
процесс называется асимптотически самоподобным второго порядка.
не зависит от
m. В этом случае,
процесс называется асимптотически самоподобным второго порядка.
Процесс
X называется точно
самоподобным второго порядка, если
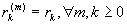
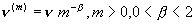 .
.
Другими словами, агрегированный процесс 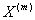 и исходный процесс X имеют схожие корреляционные структуры. Из данного
определения не следует, что самоподобный процесс действительно существует, но
фактически простые самоподобные процессы хорошо известны.
и исходный процесс X имеют схожие корреляционные структуры. Из данного
определения не следует, что самоподобный процесс действительно существует, но
фактически простые самоподобные процессы хорошо известны.
Таким образом, если исходный и агрегированный
процессы имеют одинаковые математические ожидания и ковариационные структуры,
то последовательность называется самоподобной 2-го порядка.
Чтобы выяснить смысл введенного определения, мы
рассмотрим r(t) - автокорреляционную функцию в дискретном времени.
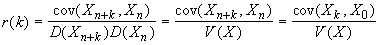
Обозначим 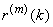 автокорреляционную
функцию последовательности
автокорреляционную
функцию последовательности 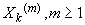 (т.е.
(т.е. 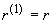 ). Для последовательности со свойством самоподобия 2-го
порядка, для любого k:
). Для последовательности со свойством самоподобия 2-го
порядка, для любого k:
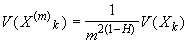 ,
, 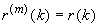
Более глубокий результат состоит в том, что функция
r(k), должна иметь определенную форму. Можно показать, что автокорреляционная
функция удовлетворяет соотношению:
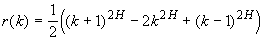 .
.
Заметим, что правая часть при больших k ведет себя
как разностное соотношение второго порядка 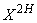 , откуда следует, что:
, откуда следует, что:
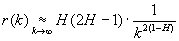
. Следовательно, можно привести следующее соотношение
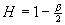
Приведем несколько примеров известных самоподобных
процессов.
Процесс 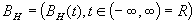 называется фрактальным броуновским движением (FBM) с параметром
самоподобия (Херста)
называется фрактальным броуновским движением (FBM) с параметром
самоподобия (Херста) 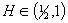 , если выполняются условия:
, если выполняются условия:
(1)
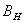 - стационарный
процесс;
- стационарный
процесс;
(2)
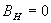 и
и 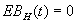
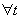 ;
;
(3)
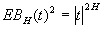
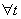 ;
;
(4)
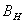 - непрерывный;
- непрерывный;
(5)
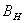 - гауссовский
процесс.
- гауссовский
процесс.
В случаях предельных значений параметра самоподобия,
процесс 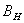 будет вести себя как
стандартный процесс броуновского движения при
будет вести себя как
стандартный процесс броуновского движения при 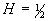 и как линейный
детерминированный процесс при
и как линейный
детерминированный процесс при 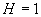 .
.
Функция ковариации для FBM положительная
и имеет следующий вид:
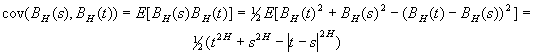
Фрактальным гауссовским шумом (FGN) называется
последовательность дискретных приращений FBM (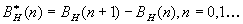 ). Ковариационная функция этого процесса совпадает с
корреляционной и имеет вид
). Ковариационная функция этого процесса совпадает с
корреляционной и имеет вид

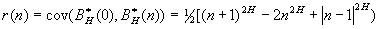 ,
, 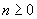 .
.
Самоподобные модели могут проявлять свойство долговременной зависимости,
что означает проявление зависимости между событиями через достаточно большие
промежутки времени. Во многих вопросах, касающихся работы с сетями, присутствие
или отсутствие долговременной зависимости играет определяющую роль в поведении,
предсказанном аналитическими моделями.
Стационарный дискретный процесс обладает
долговременной зависимостью (LRD), если автокорреляционная функция r(k) несуммируема 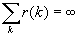 .
.
Самые простые модели с долговременной зависимостью –
самоподобные процессы, которые характеризуются гиперболически убывающими
автокорреляционными функциями. Самоподобный и асимптотически самоподобные
процессы являются особенно интересными, потому что долговременная зависимость
может характеризоваться одним параметром H, который может быть оценен. Наиболее
известными методами оценки параметра Херста H являются оценка Виттла [8] и оценка Хилла.
Рассмотрим некоторые свойства процессов с
долговременной зависимостью. Возьмем 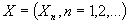 - стационарный
дискретный процесс с функцией автокорреляции r. Допустим, что процесс обладает долговременной
зависимостью, то есть
- стационарный
дискретный процесс с функцией автокорреляции r. Допустим, что процесс обладает долговременной
зависимостью, то есть 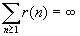 . В этом случае, автокорреляционную функцию можно представить
при помощи асимптотического приближения
. В этом случае, автокорреляционную функцию можно представить
при помощи асимптотического приближения 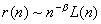 , где
, где 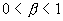
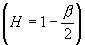 и L – мало меняющаяся функция. Тогда имеет
место
и L – мало меняющаяся функция. Тогда имеет
место
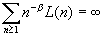 (1.2)
(1.2)
и суммируемость/несуммируемость здесь не зависит от
функции L. Это
показывает, что соотношение 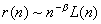 может быть использовано в качестве определения процесса с
долговременной зависимостью, который характеризуется гиперболически убывающей
автокорреляционной функцией. Заметим также, что расходимость в формуле (1.2)
гарантирует невырожденную корреляционную структуру процесса
может быть использовано в качестве определения процесса с
долговременной зависимостью, который характеризуется гиперболически убывающей
автокорреляционной функцией. Заметим также, что расходимость в формуле (1.2)
гарантирует невырожденную корреляционную структуру процесса 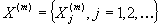 .
.
Долговременная зависимость стационарного процесса в
непрерывном времени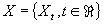 может также быть определена через автокорреляционную функцию
может также быть определена через автокорреляционную функцию
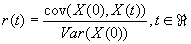 условием
условием
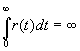 .
.
Итак,
резюмируем. Процесс X называется долговременно зависимым, если
автокорреляционная функция несуммируема 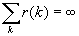 .
.
Здесь мы рассмотрим некоторые распределения с
тяжелыми хвостами, их свойства и примеры [5].
Функция
распределения имеет тяжелый хвост, если
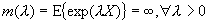 . (1.3)
. (1.3)
В
противном случае, функция распределения называется функцией с легким хвостом.
Распределение с тяжелым хвостом имеет следующее свойство:
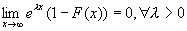 . (1.4)
. (1.4)
Рассмотрим
пример распределения с тяжелым хвостом.
Среди
функций распределения с тяжелым хвостом, рассмотрим подкласс S субэкспоненциальных
распределений. Возьмем 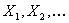 , неотрицательные, независимые одинаково
распределенные случайные величины с функцией распределения F.
, неотрицательные, независимые одинаково
распределенные случайные величины с функцией распределения F.
F называется
субэкспоненциальным распределением 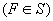 , если выполняется равенство
, если выполняется равенство
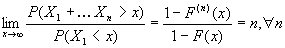 , (1.5)
, (1.5)
где
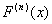 - n-мерная свертка функции
распределения F.
- n-мерная свертка функции
распределения F.
Распределения
Парето, логонормальное, Вейбулла относятся к классу субэкспоненциальных.
Функция
распределения F
с хвостом 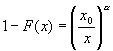 ,
, 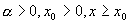 называется функцией распределения Парето.
называется функцией распределения Парето.
Случайная
величина 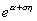 имеет логонормальное
распределение, если случайная величина
имеет логонормальное
распределение, если случайная величина 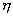 - стандартная
нормальная, т.е.
- стандартная
нормальная, т.е. 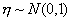 .
.
Функция
распределения F
с хвостом 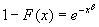 называется распределением
Вейбулла, где
называется распределением
Вейбулла, где 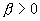 .
.
Положительная
функция L (не обязательно
монотонная) называется медленно меняющейся, если
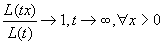
Каждая
положительная почти всюду измеримая функция медленно меняющаяся, если имеет
положительный предел при 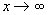 .
.
Для построения модели распределения с “тяжелым
хвостом” необходим надежный метод оценки параметра, определяющего степень
тяжести хвоста. Одной из таких оценок является оценка Хилла [1].
Потоков наборов данных, требующих распределения с
тяжелым хвостом, становится больше. Примеры этому можно найти в таких областях,
как страхование, финансовая деятельность, экономические и компьютерные
исследования, телекоммуникации.
Как уже отмечалось ранее, под распределением с
тяжелым хвостом понимаем распределение F, которое удовлетворяет следующему условию
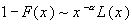
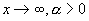 , (1.6)
, (1.6)
где L –медленно
меняющаяся функция, такая что 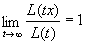 ,
, 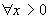 .
.
Пусть 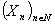 стационарная
последовательность с одномерным распределением F, таким что
стационарная
последовательность с одномерным распределением F, таким что 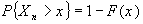 . Основная задача – это оценка необходимого параметра
. Основная задача – это оценка необходимого параметра 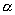 . Популярной оценкой для
. Популярной оценкой для 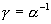 является оценка
Хилла, которая выполняется следующим образом.
является оценка
Хилла, которая выполняется следующим образом.
Пусть 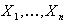 - независимые
одинаково распределенные случайные величины с функцией распределения F. Пусть
- независимые
одинаково распределенные случайные величины с функцией распределения F. Пусть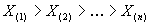 - порядковые статистики. Предположим, что F имеет тяжелый хвост:
- порядковые статистики. Предположим, что F имеет тяжелый хвост:
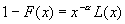 ,
, 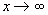 , (1.7)
, (1.7)
Функция
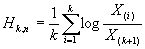 ,
, 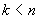 (1.8)
(1.8)
называется оценкой Хилла.
Мы используем только k порядковых
статистик, так как лучше производить выборку из той части распределения,
которая приблизительно выглядит как Парето. Объясним подробнее: набор
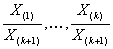
распределен как порядковые статистики из выборки
размера k и хвост
распределения имеет вид
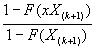 ,
, 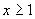 .
.
Если 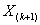 большое, то
большое, то
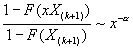 .
.
Если 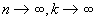 , а
, а 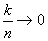 , то
, то 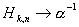 . (1.9)
. (1.9)
Из условия, накладываемого на номера порядковых
статистик, не ясно как получить результат (1.9). Здесь можно выбрать оптимальное
k, минимизирующее
среднеквадратическую ошибку.
На практике обычно строят оценку Хилла следующим
образом: по оси x откладывается k, по оси y - 
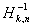 ,
, 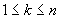 . Откуда определяют искомый параметр из устойчивой части
графика. Иногда это затрудняется тем, что выборка может быть не достаточно
большого размера и график слишком короткий. Фактически, традиционная оценка
Хилла более эффективна, если выборка имеет распределение Парето или близкое к
Парето.
. Откуда определяют искомый параметр из устойчивой части
графика. Иногда это затрудняется тем, что выборка может быть не достаточно
большого размера и график слишком короткий. Фактически, традиционная оценка
Хилла более эффективна, если выборка имеет распределение Парето или близкое к
Парето.
Для распределения Парето, 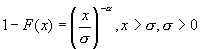 , ожидается, что график Хилла в правой части будет близок к
, ожидается, что график Хилла в правой части будет близок к 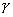 , начиная с оценки
, начиная с оценки 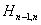 . Это следует из практики.
. Это следует из практики.
Что если график Хилла не столь информативен?
В этом случае, вместо построения 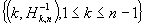 , мы строим альтернативную оценку Хилла как
, мы строим альтернативную оценку Хилла как  , где для k используется
логарифмическая шкала. Здесь наблюдается эффект растяжения левой части графика,
что дает более подробную кривую в сторону меньших значений k.
, где для k используется
логарифмическая шкала. Здесь наблюдается эффект растяжения левой части графика,
что дает более подробную кривую в сторону меньших значений k.
В процессе нахождения параметра самоподобия H возможно предположение о том, что распределение
рассматриваемых данных имеет тяжелый хвост. В этом случае, необходимо проверить
правильность предположения. Для этой цели служит описанный ниже критерий
согласия.
Предположим, что к некоторым данным было подобрано
распределение, имеющее 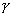 параметров.
Необходимо проверить пригодность подбора. Критерий Колмогорова-Смирнова
является непараметрическим критерием, который может быть применен для проверки
гипотезы о том, что рассматриваемая выборка
параметров.
Необходимо проверить пригодность подбора. Критерий Колмогорова-Смирнова
является непараметрическим критерием, который может быть применен для проверки
гипотезы о том, что рассматриваемая выборка 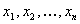 размера n взята из некоторой конкретной совокупности, которой
соответствует функция распределения F(x). Критерий
предназначен для проверки согласия эмпирической и теоретической функций
распределений.
размера n взята из некоторой конкретной совокупности, которой
соответствует функция распределения F(x). Критерий
предназначен для проверки согласия эмпирической и теоретической функций
распределений.
Критерий основывается на статистической модели,
которая предполагает непрерывность распределения, так что вероятность
совпадения выборочных значений равна нулю. Однако на практике критерий часто
применяют к сгруппированным данным и данным выборок из дискретных
распределений. В обоих случаях учитывается возможность появления равных
значений наблюдений. В данном случае уровень значимости критерия ниже
номинального, и вероятность ошибки второго рода возрастает. По всей видимости,
этот эффект не будет велик, если число оцениваемых параметров мало по сравнению
с объемом выборки.
Пусть 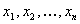 - выборка, состоящая
из n независимых
наблюдений, упорядоченных так, что
- выборка, состоящая
из n независимых
наблюдений, упорядоченных так, что 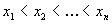 . Наблюдения независимы и берутся из генеральной
совокупности, распределение которой предполагается непрерывным.
. Наблюдения независимы и берутся из генеральной
совокупности, распределение которой предполагается непрерывным.
Гипотезы:
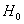 : функция распределения равна F(x);
: функция распределения равна F(x);
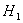 : нулевая гипотеза не верна.
: нулевая гипотеза не верна.
Критическая область – это множество таких исходов
некоторого статистического эксперимента, которые приводят нас к отклонению
нулевой гипотезы. Если нулевая гипотеза справедлива и принят уровень значимости
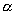 , с вероятностью
, с вероятностью 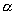 исход эксперимента
попадет в критическую область; в этом случае нулевая гипотеза будет отклонена.
В данном случае, область со значениями больше 5% - ной верхней точки
распределения Колмогорова-Смирнова будет критической. Для вычисления значений
критериальной статистики, рассчитываются кумулятивные разности:
исход эксперимента
попадет в критическую область; в этом случае нулевая гипотеза будет отклонена.
В данном случае, область со значениями больше 5% - ной верхней точки
распределения Колмогорова-Смирнова будет критической. Для вычисления значений
критериальной статистики, рассчитываются кумулятивные разности:
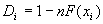
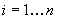
Находим значение критерия, как
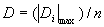 .
.
Вследствие неточностей, возникающих при определении
его уровня значимости, следует также избегать его применения при дискретных или
непрерывных сгруппированных данных. С другой стороны, можно заметить, что
альтернативный критерий не всегда отражает накопление большого числа малых
отклонений одного знака. Если регистрация такого накопления имеет значение, то
допустимо использование критерия Колмогорова-Смирнова. При этом нужно соблюдать
некоторую осторожность. Если значение статистического критерия превосходит
номинальное критическое значение, то нулевая гипотеза отклоняется. Если его
величина на много меньше номинального критического значения, следует принять
нулевую гипотезу. В том случае, когда значение критериальной статистики лишь
немного меньше номинального, нужно быть осторожным в принятии определенного
решения.
В этом параграфе хотелось бы остановиться на кратком
описании уже существующих разработок для исследования поведения сетевого
трафика. Такие исследования широко проводятся некоторыми западными
исследовательскими и образовательными учреждениями, такими как Университет в
Бостоне, Университет Беркли, Университет Северной Каролины и другие. Приведем
описание ряда проблем, затронутых в некоторых работах этих исследовательских
центров и касающихся рассматриваемой нами тематики. Множество исследований были
проведены для локальных компьютерных сетей. Одним из первых анализ высокой
точности трафика Ethernet LAN был проведен Уиллом Леландом и Даниэлем Уилсоном
в 1991 году. Эти данные состояли из сотни миллионов пакетов[11]. Далее этими же исследователями на основе той же
большой выборки была проведена работа, которая устанавливает, что сетевой
трафик передачи пакетов имеет самоподобные характеристики. Важность этой работы
заключается в том, что получено подтверждение предположения относительно не
точности моделирования сетевого трафика при помощи, использовавшегося ранее
Пуассоновского распределения данных[12]. За исследованиями локальных сетей появились
разработки по анализу трафика глобальной сети, и в частности WWW. Одной из последних работ в этой области являются
исследования Марка Кровеллы и Айзера Беставроса, которые представляют собой подтверждение
самоподобия в WWW-трафике[4]. Для исследования используется месячный массив
WWW-запросов, взятых в университетской компьютерной лаборатории. Показывается,
что самоподобие в WEB-трафике
может быть объяснено распределением размеров переданного документа, эффектах
кэширования и настройках пользователя по передаче файла, человеческом факторе,
а также суперпозицией множества таких передач в локальной сети. Это является
очень интересным результатом, который представляет собой уже следующий шаг, а
именно изучение причин проявления именно самоподобной структуры сетевого
трафика. Основываясь на методологии, приведенной этих работах, мы решили
провести исследования поведения трафика WWW-запросов реально существующего
ресурса.
Для осуществления цели работы, а именно,
подтверждения существования свойства самоподобия при моделировании поведения
трафика глобальной сети, необходимо произвести измерения некоторых характеристик
реального сетевого ресурса. Рассматриваемый объект представляет собой
веб-ресурс глобальной сети Интернет. Объект является представительством в сети
Интернет популярного периодического издания “Комсомольская Правда” в Карелии”,
и содержит порядка 10 основных разделов, таких как “Главная страница”, “Архив
статей”, “Анонсы”, “Конкурс”, “Гороскоп”, “Редакция”, “Рекламный отдел”.
Для более полного представления о ресурсе приведем
некоторые статистические данные. Количество посетителей за период существования
около 15000. При этом количество посетителей, составляющих ядро аудитории, то
есть обращающихся к серверу не менее двух раз в неделю на протяжении месяца
составляет на сегодняшний день 397 человек. Интересна статистика посещения
ресурса с точки зрения географического распределения аудитории.
Таблица 1 Распределение аудитории
сайта по странам (первая пятерка по популярности)
Таблица 2 Распределение аудитории
сайта по городам (первая пятерка по популярности)
Сайт управляется веб-сервером Apache. Все действия сервера записываются в так называемый
лог-файл. Лог-файл состоит из строк следующего типа:
62.54.225.107
- - [26/Apr/2001:04:34:13 +0400] "GET /styles.css HTTP/1.1" 200 8251
Лог-файлы хранятся в течении трех дней, затем
удаляются из-за достижения достаточно большого объема.
Вся текстовая информация сайта хранится в базе
данных. При обращении к странице сайта исполняется SQL-запрос, который возвращает необходимую информацию.
Все страницы сайта имеют схожую структуру, которая представляет собой набор
скриптов, осуществляющих динамическую компоновку страницы по запросу клиента.
Ресурс существует в сети Интернет с сентября 2000
года. Необходимыми данными для наших исследований является количество запросов
к серверу. Получить эти данные можно при помощи анализа лог-файла. Период исследования
включает четыре месяца с февраля по май 2001 года включительно.
Рассмотрим данные, которые представляют собой
количество запросов пользователей к серверу в течение часа за период длиной 4
месяца с 1 февраля 2001 года по 31 мая 2001 года (рис. 2.1). Это одни из
возможных данных о трафике сети. Так же можно рассматривать размеры
передаваемых файлов, интервалы передачи и другие возможные характеристики
сетевого трафика. К ним применимы методы, описываемые здесь.
Полученный временной ряд состоит из 2830 наблюдения,
каждое из которых представляет собой количество запросов пользователя в течение
часа 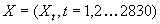 . Осуществим с имеющимся временным рядом следующий агрегационный
процесс. Выполним уменьшение размера шкалы наблюдений в 5 раз. Для этого
вычислим новый ряд, полученный при помощи операции нахождения среднего каждых 5
последовательных исходных наблюдений.
. Осуществим с имеющимся временным рядом следующий агрегационный
процесс. Выполним уменьшение размера шкалы наблюдений в 5 раз. Для этого
вычислим новый ряд, полученный при помощи операции нахождения среднего каждых 5
последовательных исходных наблюдений.
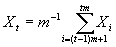 ,
,
где m – число
усредняемых последовательных членов ряда.
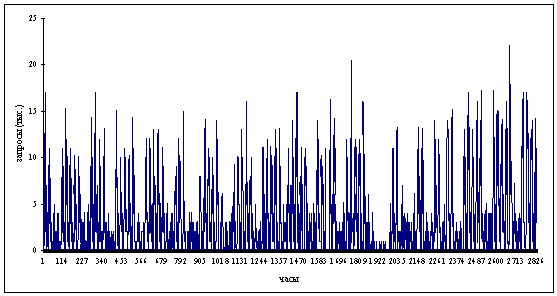
Рисунок 2.1 Трафик. Период 2830 часов
Новый ряд будет состоять из 556 событий (рис. 2.2).
То есть фактически произошло уменьшение рассматриваемой шкалы в 5 раз. Это
означает, что каждое единичное деление новой шкалы содержит 5 единиц исходной.
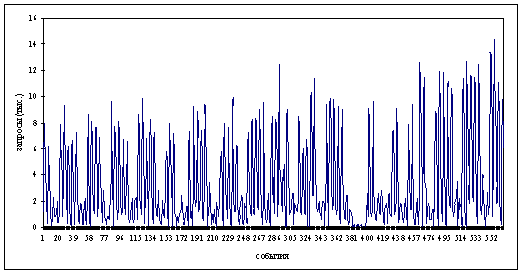
Рисунок 2.2 Объединение данных по 5
часов
Далее, проделаем такую же процедуру с исходным рядом,
но уменьшив значения делений уже в 10 раз (рис. 2.3). Таким образом, одно
деление будет содержать 10 единиц исходной. Завершим преобразования еще одной
итерацией, аналогичной предыдущей, где единица итоговой шкалы будет
соответствовать 15 единицам исходной (рис. 2.4).
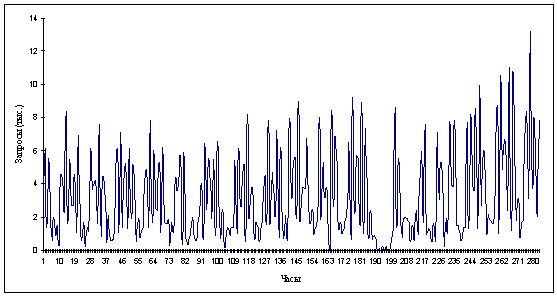
Рисунок 2.3 Объединение данных по 10
часов
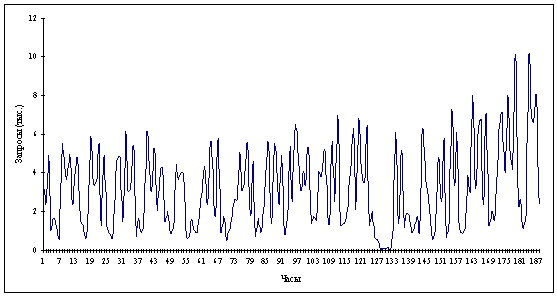
Рисунок 2.4 Объединение данных по 15
часов
Проанализируем полученные результаты. Основываясь на
работах западных исследователей [4], мы можем высказать предположение о том, что
рассматриваемый нами трафик имеет самоподобную структуру. Этот вывод можно
сделать исходя из определения самоподобия, которое говорит о том, что структура
ряда, полученного усреднением групп элементов остается такой же, как и
структура исходного. Этот эффект мы можем наблюдать на графиках,
иллюстрирующих, рассмотренное выше изменение шкалы. Этот факт является
предпосылкой для предположения о самоподобной структуре рассматриваемого
трафика и основанием для проведения дальнейшего более полного анализа.
Предполагаем, что распределение наших данных является
распределением с тяжелым хвостом. Распределение имеет тяжелый хвост, если
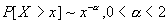 .
.
Простейшим распределением с тяжелым хвостом является
распределение Парето, для которого функция плотности распределения имеет вид 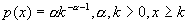 и функция
распределения
и функция
распределения 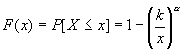 .
.
Распределение с тяжелым хвостом имеет ряд свойств,
которые существенно отличают его от наиболее известных распределений, таких как
экспоненциальное, нормальное или пуассоновское.
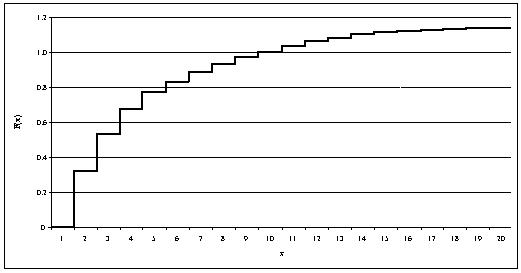
Рисунок 2.5 Эмпирическая функция
распределения
Если 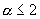 , тогда распределение имеет бесконечную дисперсию; если
, тогда распределение имеет бесконечную дисперсию; если 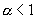 , то распределение имеет бесконечное среднее. При уменьшении
, то распределение имеет бесконечное среднее. При уменьшении 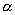 , произвольная большая порция плотности может быть
представлена в хвосте распределения. Фактически, тяжелый хвост означает наличие
бесконечной дисперсии, иначе говоря, случайная величина может принимать очень
большие значения, но с очень маленькой вероятностью.
, произвольная большая порция плотности может быть
представлена в хвосте распределения. Фактически, тяжелый хвост означает наличие
бесконечной дисперсии, иначе говоря, случайная величина может принимать очень
большие значения, но с очень маленькой вероятностью.
Чтобы оценить тяжесть хвоста для имеющихся данных, мы
строим график дополнительного распределения 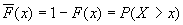 . Для этого строим дискретную эмпирическую функцию
распределения для наших данных (рис. 2.5). Разделим наши данные на 943
непересекающихся интервала. Вычислим частоты попадания в каждый интервал.
Далее, построим новый ряд, вычислив среднее значение в каждом интервале и
соответствующую частоту.
. Для этого строим дискретную эмпирическую функцию
распределения для наших данных (рис. 2.5). Разделим наши данные на 943
непересекающихся интервала. Вычислим частоты попадания в каждый интервал.
Далее, построим новый ряд, вычислив среднее значение в каждом интервале и
соответствующую частоту.
Полученная функция распределения, позволяет
рассчитать значения дополнительной функции распределения и построить ее график
в логарифмической шкале (рис. 2.6).
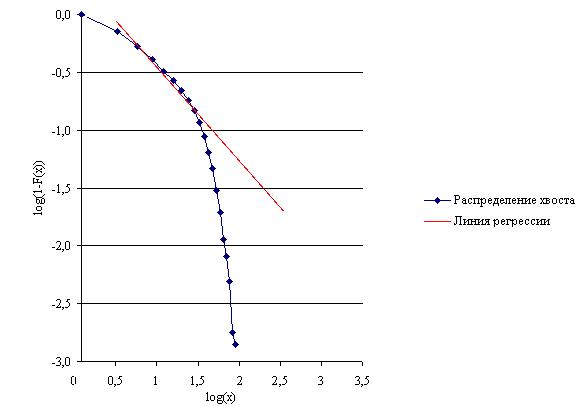
Рисунок 2.6 Функция распределения
хвоста
Значение коэффициента 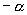 , являющееся оценкой тяжести хвоста распределения, будет
соответствовать
, являющееся оценкой тяжести хвоста распределения, будет
соответствовать 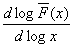 . Построив линию регрессии для дополнительной функции
распределения и вычислив тангенс угла наклона к горизонтальной оси, мы получим
значение параметра
. Построив линию регрессии для дополнительной функции
распределения и вычислив тангенс угла наклона к горизонтальной оси, мы получим
значение параметра 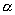 . В нашем случае,
. В нашем случае, 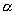 принимает значение
равное 1,14. Значение попадает в промежуток от 0 до 2, откуда следует, что наше
распределение имеет свойство тяжелого хвоста. Причем, чем меньше значение
принимает значение
равное 1,14. Значение попадает в промежуток от 0 до 2, откуда следует, что наше
распределение имеет свойство тяжелого хвоста. Причем, чем меньше значение 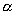 , тем более тяжелым будет хвост.
, тем более тяжелым будет хвост.
Существует также другая возможность оценить параметр тяжести хвоста распределения, называемая
оценкой Хилла. Для ее проведения нам понадобится упорядочить множество наших
данных по возрастанию 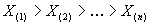 , получив набор порядковых статистик. Далее, вычислим функцию
Хилла
, получив набор порядковых статистик. Далее, вычислим функцию
Хилла 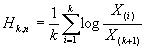 для
для 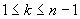 (рис. 2.7).
(рис. 2.7).
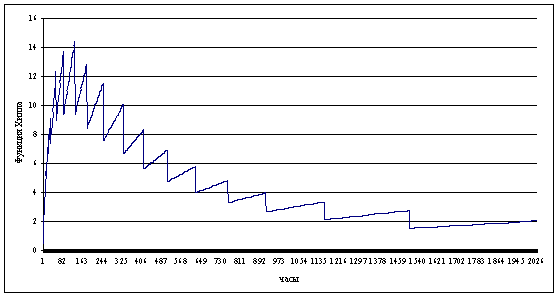
Рисунок 2.7 Функция Хилла
Теперь, глядя на график можно определить значение,
начиная с которого, поведение функции стабилизируется. Значение функции Хилла в
этой точке будет равно искомому параметру 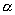 . Сложность данного метода заключается в трудности
определения момента начала стабилизации поведения функции Хилла. Поэтому мы не
рассматриваем этот метод в качестве способа оценки пара мера тяжести хвоста.
. Сложность данного метода заключается в трудности
определения момента начала стабилизации поведения функции Хилла. Поэтому мы не
рассматриваем этот метод в качестве способа оценки пара мера тяжести хвоста.
Мы предположили, что выборка имеет распределение с
тяжелым хвостом. С помощью метода Колмогорова-Смирнова проверим нулевую
гипотезу предполагающую, что выборка имеет распределение с тяжелым хвостом с
параметром 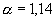 , который мы вычислили ранее.
, который мы вычислили ранее.
Начнем с упорядочивания наблюдений по возрастанию, а
затем вычислим наблюдаемые и ожидаемые значения, которые меньше каждого
наблюдения или равны ему. Максимальная абсолютная величина разности между ними
будет равна 19,0521 и значение критериальной статистики равно
D=19,817/2831=0,007
Так как число наблюдений достаточно велико, 5%-ное
критическое значение вычисляем следующим приближением
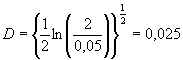 .
.
Значение критерия 0,007 намного меньше номинального
критического значения 0,025. Поэтому мы принимаем нулевую гипотезу и заключаем,
что неизвестное распределение является распределением с тяжелым хвостом с
параметром 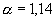 .
.
Понятие тяжелого хвоста означает, что дополнительная
функция распределения с тяжелым хвостом убывает медленнее, чем экспоненциальное
распределение (рис. 2.8).
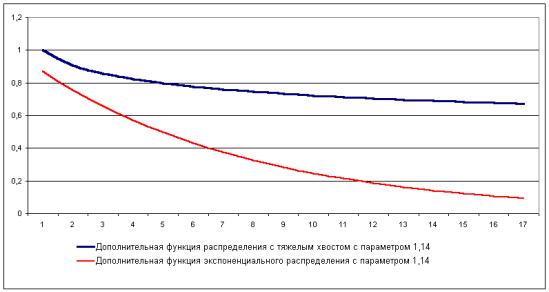
Рисунок 2.8 Сравнение распределения
с тяжелым хвостом
и экспоненциального распределения
Существует
ряд методов, позволяющих выполнить проверку свойства самоподобия исследуемого
процесса [3]. Первый метод, это построение графика функции распределения для
процесса из непересекающихся групп, объединяющих события исходного процесса.
График строится по логарифмической шкале и наклон линии регрессии позволяет
вычислить параметр 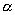 , через который выражается параметр самоподобия
, через который выражается параметр самоподобия 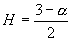 . Другой метод – метод периодограммы –использует в
оценке наклон спектральной функции при частоте, стремящейся к нулю. Еще один
метод, называемый оценкой Виттла, дает доверительный интервал для параметра
самоподобия, но имеет существенный недостаток в том, что вид стохастического
процесса должен быть определен. Два вида, которые обычно используются, это
фрактальный Гауссовский процесс (FGN)
с параметром
. Другой метод – метод периодограммы –использует в
оценке наклон спектральной функции при частоте, стремящейся к нулю. Еще один
метод, называемый оценкой Виттла, дает доверительный интервал для параметра
самоподобия, но имеет существенный недостаток в том, что вид стохастического
процесса должен быть определен. Два вида, которые обычно используются, это
фрактальный Гауссовский процесс (FGN)
с параметром 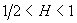 и фрактальный
процесс ARIMA(p,d,q) с
и фрактальный
процесс ARIMA(p,d,q) с 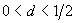 [6].
[6].
В
данной работе мы использовали первый метод для оценки параметра 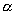 , и теперь можем получить значение параметра
самоподобия
, и теперь можем получить значение параметра
самоподобия 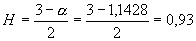 . Значение параметра самоподобия попадает в
промежуток от ½ до
. Значение параметра самоподобия попадает в
промежуток от ½ до 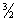 , что означает подтверждение предполагаемого на
первом шаге исследования свойства самоподобия рассматриваемого процесса.
, что означает подтверждение предполагаемого на
первом шаге исследования свойства самоподобия рассматриваемого процесса.
В
работах западных исследователей можно также встретить следующий способ
выявления свойства самоподобия исследуемого процесса. Рассчитав параметр
самоподобия H,
мы будем использовать его при увеличении масштаба шкалы. Воспользуемся
следующим процессом для получения усредненных данных для шкалы более крупного
масштаба 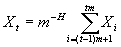 . Проведем три итерации для значений m=5, 10, 15 (Рис. 2.9, Рис
2.10, Рис 2.11).
. Проведем три итерации для значений m=5, 10, 15 (Рис. 2.9, Рис
2.10, Рис 2.11).
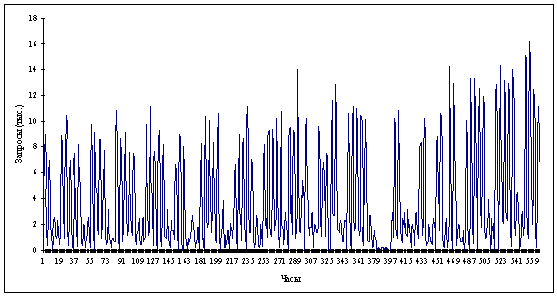
Рисунок 2.9 Объединение данных по 5
часов с H=0,93
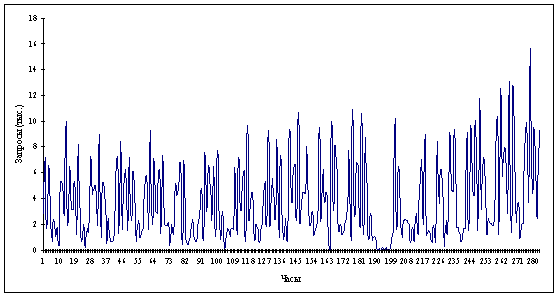
Рисунок 2.10 Объединение данных по
10 часов с H=0,93
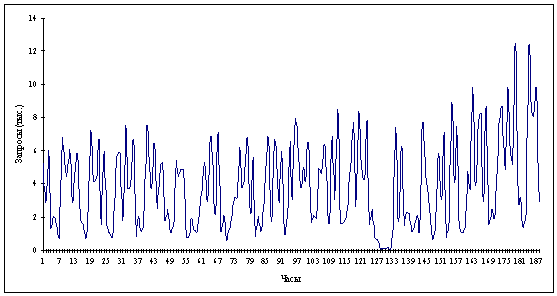
Рисунок 2.11 Объединение данных по
15 часов с H=0,93
Этот
способ позволяет проиллюстрировать свойство самоподобия. Визуальным наблюдением
агрегированных процессов полученных с параметром H можно
сделать вывод о сохранении структуры процесса.
Рассматривая
автокорреляционные функции исходного и агрегированных рядов, можно заметить что
автокорреляционная структура процесса сохраняется. В Приложении 2 представлен
график автокорреляционной функции для оригинального ряда. Это еще раз
показывает, что процесс обладает свойством самоподобия.
Таким образом, параметр самоподобия, рассматриваемого
процесса находится в диапазоне от ½ до 1. Это означает, что самоподобный
процесс обладает свойством долговременной зависимости. Для процесса с
долговременной зависимостью автокорреляционная функция приближается функцией
вида
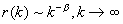 , где
, где 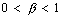 .
.
Ранее мы оценили параметр 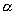 для нашей выборки.
Параметр
для нашей выборки.
Параметр 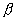 для
автокорреляционной функции связан с параметром
для
автокорреляционной функции связан с параметром 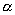 следующим
соотношением
следующим
соотношением 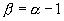 . В нашем случае
. В нашем случае 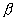 =0,14.
=0,14.
В
данной работе было проведено исследования сетевого трафика. Главным
направлением исследования являлось выявление свойства самоподобия веб-трафика.
С этой целью была проведена статистическая обработка данных выбранного
веб-ресурса рядом методов.
Предположение
о самоподобной структуре веб-трафика основывается на рассмотрении имеющихся
данных для различной временной шкалы. Далее, мы выдвигаем гипотезу о том, что
распределение процесса является распределением с тяжелым хвостом. Используя
метод построения дополнительной функции распределения для логарифмической
шкалы, вычисляем параметр 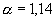 , оценивающий тяжесть хвоста. Делаем вывод о том, что
функция распределения действительно имеет достаточно тяжелый хвост. Для
проверки принятия гипотезы используем критерий согласия Колмогорова-Смирнова.
При помощи известного параметра
, оценивающий тяжесть хвоста. Делаем вывод о том, что
функция распределения действительно имеет достаточно тяжелый хвост. Для
проверки принятия гипотезы используем критерий согласия Колмогорова-Смирнова.
При помощи известного параметра 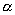 вычисляем
параметр самоподобия H=0,93.
Используя полученные результаты, проверяем свойство самоподобия
рассматриваемого процесса согласно определению.
вычисляем
параметр самоподобия H=0,93.
Используя полученные результаты, проверяем свойство самоподобия
рассматриваемого процесса согласно определению.
Таким
образом, получено подтверждение предположения о самоподобии сетевого трафика
веб-ресурса. Этот результат не является доказательством самоподобной структуры
сетевого трафика. Исследуемый процесс является только одним из возможных
случаев поведения трафика.
В дальнейших разработках будет интересно
провести подобные исследования для анализа других видов трафика. А так же
применить дополнительные методы для определения параметров самоподобия.
Интересным вопросом является изучение причин возникновения самоподобия в
сетевом трафике.
Подобные
исследования необходимы для понимания поведения сетевого трафика, и возможно,
разработок новых моделей.
[1]
Holger Drees, Laurents de Haan, and Sidney Resnick, “How
to make a Hill Plot”, Sept. 1998.
[2]
Evsei V. Morozov “Self-Similarity and Long-Range Dependce
in Network Traffic Modeling” Proceedings of FDPW’99 “Developments in
Distributed Systems and data Communications”, Vol. 2, pp. 32-40, 1999.
[3]
Irina V. Aminova “Queueing Networks Simulation: Artificial
Regeneration and Heavy Tail Phenomena” Proceedings of FDPW’99 “Developments in
Distributed Systems and data Communications”, Vol. 2, pp. 125-136, 1999.
[4]
Mark E. Crovella and Azer Bestavros, “Self-Similarity in
World Wide Web Traffic: Evidence and Possible Causes” in IEEE/ACM Transactions
on Networking, 5(6):835--846, December 1997.
[5]
Mark E. Crovella, Murad Taqqu and Azer Bestavros, “Heavy
Tailed-Probability distributions in the World Wide Web” 5(6):835--846, December
1997.
[6]
Mark E. Crovella, Azer Bestavros, Paul Baarfor, Adam
Bradley “Change in Web Client Access Patterns. Characteristics and Caching
Implications”,Computer Science Department Boston University, 1999.
[7]
Vern Paxson and Sally Floyd, “Wide-Area Traffic: The
Failure of Poisson Modeling” IEEE/ACM Transactions on Networking, Vol. 3 No. 3,
pp. 226-244, June 1995.
[8]
Vern Paxson, “Fast, Approximate Synthesis of Fractional Gaussian Noise for Generating
Self-Similar Network Traffic”. Computer Communications Review, V. 27 N. 5,
October 1997, pp. 5-18.
[9]
Walter Willinger, Murad Taqqu, Robert Sherman, and Daniel
Wilson, Self-Similarity Through High-Variability: Statistical Analysis of
Ethernet LAN Traffic at the Source Level” IEEE/ACM Transactions on Networking,
Vol. 5, No. 1, pp. 71-86, February
1997
[10]
Walter Willinger, Vern Paxson, and Murad Taqqu,
“Self-similarity and Heavy Tails: Structural Modeling of Network Traffic”.
[12]
Will Leland, Murad Taqqu, Walter Willinger, and Daniel
Wilson, “On the Self-Similar Nature of Ethernet Traffic”, IEEE/ACM Transactions
on Networking, Vol. 2, No. 1, pp. 1-15, February 1994.
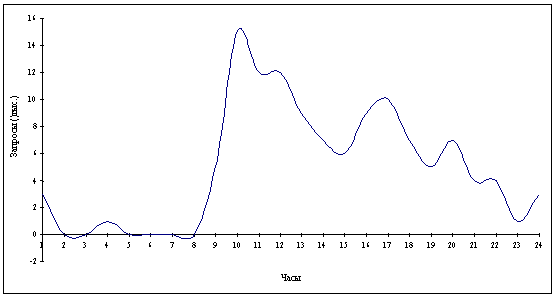
Рисунок 1.1 Распределение запросов по
часам за период времени 1 сутки
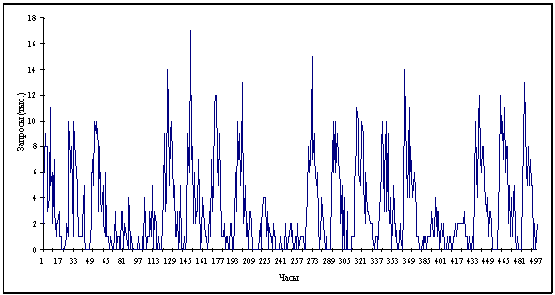
Рисунок 1.2 Распределение запросов по
часам за период времени 1 месяц
Рисунок 2.1 Автокорреляционная
функция

![]() - стационарный
второго порядка, если выполняются условия:
- стационарный
второго порядка, если выполняются условия:![]() – самоподобный
процесс с параметром H, если
распределения
– самоподобный
процесс с параметром H, если
распределения ![]() и
и ![]() эквивалентны для
любого Т>0.
эквивалентны для
любого Т>0.![]() , L(k) – мало меняющаяся
функция.
, L(k) – мало меняющаяся
функция.![]() , если выполняется равенство
, если выполняется равенство![]() - n-мерная свертка функции
распределения F.
- n-мерная свертка функции
распределения F.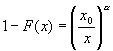 ,
, ![]() называется функцией распределения Парето.
называется функцией распределения Парето.![]() называется распределением
Вейбулла, где
называется распределением
Вейбулла, где ![]() .
.![]() ,
, ![]() .
.![]() : функция распределения равна F(x);
: функция распределения равна F(x);